Sekante
Sekante Definition
Eine Sekante (von lateinisch secare für schneiden) ist eine Gerade, die eine Funktionskurve in zwei (oder mehr) Punkten schneidet.
Man kann sich hier das durchhängende Seil einer Seilbahn als Funktionskurve vorstellen und einen (ungefährlichen) Laserstrahl, der durch 2 Punkte der Seilbahn geht, als Gerade.
Sekante berechnen
Für eine Funktion kann man die Sekante bzw. die Gleichung der Sekante wie folgt berechnen:
Beispiel: Sekantengleichung berechnen
Die Funktion sei f(x) = x2 + 2x.
Es soll die Gleichung der Sekante berechnet werden, welche durch die Punkte für x1 = 1 und x2 = 2 geht.
Zunächst x1 = 1 in die Funktion einsetzen: f(1) = 12 + 2 × 1 = 1 + 2 = 3.
Ebenso x2 = 2 in die Funktion einsetzen: f(2) = 22 + 2 × 2 = 4 + 4 = 8.
D.h., die Sekante geht durch die Punkte (1, 3) und (2, 8).
Nun muss noch die Steigung der Sekante berechnet werden.
Sekantensteigung berechnen
Die Sekantensteigung bzw. mittlere Steigung entspricht dem Differenzenquotienten:
Sekantensteigung = f(x2) - f(x1) / x2 - x1 = (8 - 3) / (2 - 1) = 5/1 = 5.
Diese Sekantensteigung gibt an, wie sich der Funktionswert zwischen den beiden Punkten x1 = 1 und x2 = 2 ändert, nämlich um 5 (von 3 auf 8).
Allgemein hat eine Gerade (damit auch die Sekante) die Form y = m × x + b (vgl. Lineare-Funktion).
Dabei ist m die Steigung (also 5, wie oben berechnet) und b der Schnittpunkt mit der y-Achse (noch unbekannt).
Man kann jetzt z.B. x1 = 1 und den Funktionswert f(1) = 3 in die Geradengleichung einsetzen:
3 = 5 × 1 + b; daraus folgt: b = -2
Die Sekantengleichung kann man mit s(x) bezeichnen, sie lautet dann: s (x) = 5 × x - 2.
Die Funktion und die Sekante in der Grafik:
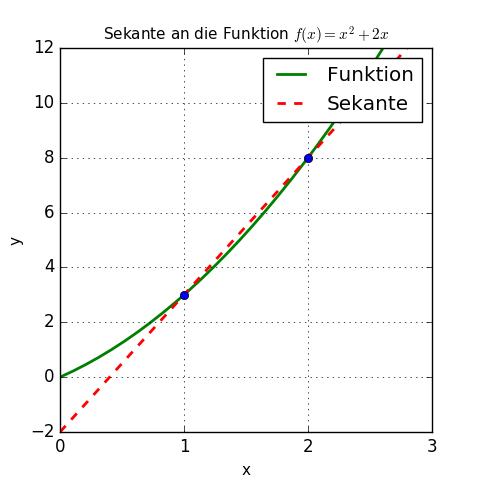
Das ist nur eine Sekante durch zwei Punkte; es gibt natürlich viele Möglichkeiten, eine Funktionskurve durch andere Punkte zu schneiden.
In der Analysis interessiert man sich eher für einen Spezialfall der Sekante: man nähert den zweiten Punkt ganz nah an den ersten (z.B. indem man statt x2 = 2 dann x2 = 1,01 oder noch näher verwendet), die Sekante wird dadurch zu einer Tangente, welche die Funktionskurve nicht mehr schneidet, sondern im Punkt x1 = 1 berührt; damit hat man die Steigung an der Stelle x1 = 1 und damit die Ableitung der Funktion an der Stelle.