Bestimmtheitsmaß
Bestimmtheitsmaß Definition
Im Beispiel zur Methode der kleinsten Quadrate (lineare Regression) wurde ein linearer Zusammenhang zwischen der abhängigen Variablen (Schuhgröße y) und der unabhängigen Variablen (Körpergröße x) mit der Regressionsfunktion yi = 34 + 0,05 × xi abgebildet.
Nun stellt sich die Frage, wie gut diese Regressionsgerade ist, das heißt wie nahe liegen die sich aus der gefundenen Regressionsfunktion ergebenden Werte für die Schuhgröße in Abhängigkeit von der Körpergröße den tatsächlich gemessenen Schuhgrößen.
Mit anderen Worten: Wie gut wird die Punktewolke durch die Regressionsgerade angenähert?
Diese Frage kann durch das Bestimmtheitsmaß als "Gütemaß der Regression" beantwortet werden.
Dazu setzt man die durch die Regressionsfunktion erklärte Streuung der Daten (berechnet als quadrierte Abstände) zu der gesamten Streuung in Relation.
Alternative Begriffe: Determinationskoeffizient.
Beispiel
Beispiel: Bestimmtheitsmaß berechnen
Auf die Daten zur Methode der kleinsten Quadrate bezogen:
| Person | Körpergröße in cm (xi) | Schuhgröße (yi) |
|---|---|---|
| Anton | 170 | 42 |
| Bernd | 180 | 44 |
| Claus | 190 | 43 |
Die Regressionsgerade lautete: yi = α + β × xi = 34 + 0,05 × xi.
Schritt 1: Gesamtstreuung berechnen
Die quadrierten Abstände zwischen den tatsächlichen Schuhgrößen und dem Mittelwert der Schuhgröße (der Mittelwert ist: (42 + 44 + 43) / 3 = 43) sind in Summe: (42 - 43)2 + (44 - 43)2 + (43 - 43)2 = -12 + 12 + 02 = 1 + 1 + 0 = 2.
Schritt 2: durch Regression erklärte Streuung berechnen
Aus der Regressionsfunktion ergeben sich folgende "prognostizierte" y-Werte (Schuhgrößen):
y1 = 34 + 0,05 × 170 = 34 + 8,5 = 42,5
y2 = 34 + 0,05 × 180 = 34 + 9 = 43
y3 = 34 + 0,05 × 190 = 34 + 9,5 = 43,5
Die quadrierten Abstände zwischen den prognostizierten Schuhgrößen und dem Mittelwert der Schuhgröße sind in Summe: (42,5 - 43)2 + (43 - 43)2 + (43,5 - 43)2 = -0,52 + 02 + 0,52 = 0,25 + 0 + 0,25 = 0,5.
Schritt 3: Bestimmtheitsmaß berechnen
Bestimmheitsmaß = erklärte Streuung / gesamte Streuung = 0,5 / 2 = 0,25.
Interpretation
Das Bestimmtheitsmaß liegt immer im Intervall 0 bis 1.
Je näher das Bestimmtheitsmaß an 1 dran ist, desto besser passt die ermittelte Regressionsgerade (bei einem Bestimmtheitsmaß von 1 sind alle Residuen 0).
Je näher das Bestimmtheitsmaß an 0 ist, desto schlechter passt sie, so wie hier mit 0,25.
Dass die Regression nicht gut ist sieht man schon grafisch an der Regressionsgeraden im Streudiagramm bzw. den Abständen zu den Daten:
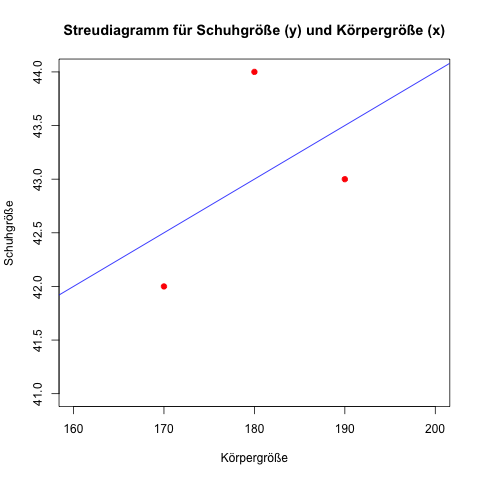
Die unabhängige Variable „Körpergröße“ kann also nur 25 % der Unterschiede der abhängigen Variablen „Schuhgröße“ erklären – im Umkehrschluss können damit 75 % der Unterschiede nicht erklärt werden.
Alternative Berechnung: Quadrierter Korrelationskoeffizient
Im Falle der einfachen linearen Regression (so wie hier im Beispiel) entspricht das Bestimmtheitsmaß dem quadrierten Korrelationskoeffizienten (nach Pearson).
Dieser wäre 0,5 und quadriert ergibt sich auch daraus das Bestimmtheitsmaß R2 = 0,52 = 0,25.
Bei multiplen linearen Regressionen (bei denen zum Beispiel neben der Körpergröße noch die Handschuhgröße als zweite unabhängige Variable für die Vorhersage der Schuhgröße mittels Regression genutzt würde) geht das nicht.