Chi-Quadrat-Verteilung
Chi-Quadrat-Verteilung Definition
Die Chi-Quadrat-Verteilung – kurz: χ2-Verteilung – gehört zu den stetigen Testverteilungen, sie hat nur einen Parameter: die Anzahl der Freiheitsgrade.
Die Chi-Quadrat-Verteilung ist für kleine Freiheitsgrade eine rechtsschiefe Verteilung, mit zunehmender Anzahl der Freiheitsgrade nähert sich die Form der Chi-Quadrat-Verteilung der Normalverteilung, d.h. einer symmetrischen Verteilung, an.
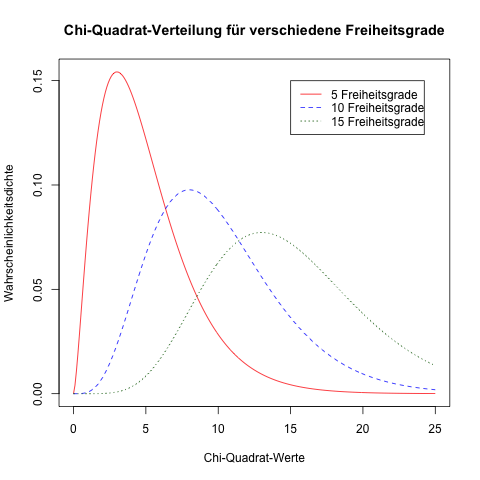
Die Gesamtfläche unterhalb der Chi-Quadrat-Verteilung ist (wie immer bei stetigen Verteilungen) 1.
Die Werte χ2 der Chi-Quadrat-Verteilung sind alle positiv und werden i.d.R. einer Tabelle entnommen oder mit einem Statistikprogramm berechnet.
Auf der Chi-Quadrat-Verteilung beruhen mehrere Tests:
Chi-Quadrat-Tabelle
In der folgenden Chi-Quadrat-Verteilungstabelle (Ausschnitt; gerundet auf 3 Nachkommastellen) stehen in den Zeilen die unterschiedlichen Freiheitsgrade (hier von 1 bis 15), in den Spalten die jeweiligen kritischen rechts liegenden Bereiche.
Ist der Stichprobenumfang z.B. 10, ist die Anzahl der Freiheitsgrade 10 - 1 = 9. Ist das Signifikanzniveau 0,05 bei einem einseitigen Test, ist der Wert in der dazugehörigen Spalte zu suchen; der Wert in der Tabelle ist 16,919.
| 0,975 | 0,95 | 0,05 | 0,25 | |
|---|---|---|---|---|
| 1 | 0,001 | 0,004 | 3,841 | 5,024 |
| 2 | 0,051 | 0,103 | 5,991 | 7,378 |
| 3 | 0,216 | 0,352 | 7,815 | 9,348 |
| 4 | 0,484 | 0,711 | 9,488 | 11,143 |
| 5 | 0,831 | 1,145 | 11,070 | 12,833 |
| 6 | 1,237 | 1,635 | 12,592 | 14,449 |
| 7 | 1,690 | 2,167 | 14,067 | 16,013 |
| 8 | 2,180 | 2,733 | 15,507 | 17,535 |
| 9 | 2,700 | 3,325 | 16,919 | 19,023 |
| 10 | 3,247 | 3,940 | 18,307 | 20,483 |
| 11 | 3.816 | 4,575 | 19,675 | 21,920 |
| 12 | 4,404 | 5,226 | 21,026 | 23,337 |
| 13 | 5,009 | 5,892 | 22,362 | 24,736 |
| 14 | 5,629 | 6,571 | 23,685 | 26,119 |
| 15 | 6,262 | 7,261 | 24,996 | 27,488 |