Wahrscheinlichkeitsverteilung
Wahrscheinlichkeitsverteilung Definition
Eine Wahrscheinlichkeitsverteilung ordnet den möglichen Ergebnissen einer Zufallsvariablen eine Wahrscheinlichkeit zu.
Beispiel
Das Zufallsexperiment sei "2-maliger Münzwurf" (mit einer spanischen 1-Euro-Münze mit der Vorderseite "Zahl" und der Rückseite "Kopf") und die Zufallsvariable sei "Anzahl der Köpfe".
Die Zufallsvariable kann die Werte 0 (Zahl und Zahl), 1 (Kopf und Zahl oder Zahl und Kopf) und 2 (Kopf und Kopf) annehmen.
Die Wahrscheinlichkeitsverteilung (oft auch als Tabelle dargestellt) ist dann:
- 0: 1/4 = 0,25
- 1: 1/4 + 1/4 = 2/4 = 1/2 = 0,5
- 2: 1/4 = 0,25.
Die Wahrscheinlichkeitsverteilung als Grafik:
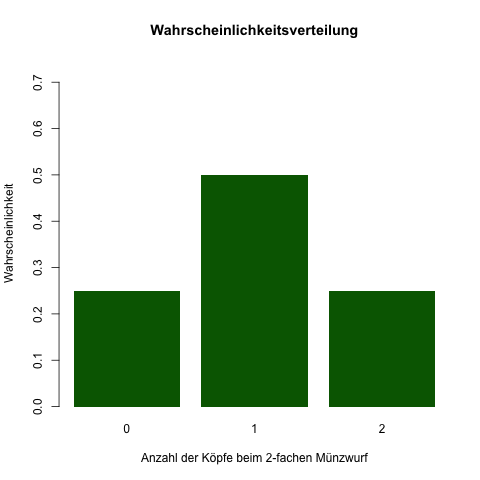
Die Wahrscheinlichkeitsverteilung gibt also jeweils die Wahrscheinlichkeit für einen bestimmten Wert der Zufallsvariablen an (z.B. "Anzahl der Köpfe" = 1); möchte man eine "Höchstens"-Wahrscheinlichkeit (z.B. "Anzahl der Köpfe" = maximal 1), benötigt man die Verteilungsfunktion, die die Wahrscheinlichkeiten kumuliert (im Beispiel: 1/4 + 2/4 = 3/4).
Die Wahrscheinlichkeiten der Wahrscheinlichkeitsverteilung addieren sich immer auf 1 (bzw. 100 %).
Viele Fragestellungen laufen auf dieselben, standardmäßigen Wahrscheinlichkeitsverteilungen bzw. Verteilungsmodelle hinaus. Je nachdem, ob die zugrundeliegenden Zufallsvariablen diskret oder stetig sind, unterscheidet man diskrete und stetige Wahrscheinlichkeitsverteilungen.
Diskrete Wahrscheinlichkeitsverteilungen
Dazu zählen:
- Diskrete Gleichverteilung: für den Fall, dass jedes Ergebnis dieselbe Wahrscheinlichkeit hat (Münze, Würfel, Glücksrad mit gleich großen Feldern);
- Binomialverteilung: für Zufallsexperimente mit nur 2 möglichen Ergebnissen (z.B. "Kopf oder Zahl", "Medikament wirkt oder wirkt nicht", "Elfmeter verwandelt oder nicht", etc.) unter "Ziehen mit Zurücklegen";
- Multinomialverteilung: als Verallgemeinerung der Binomialverteilung für Zufallsexperimente mit mehr als 2 möglichen Ergebnissen (z.B. Würfel mit 6 Augenzahlen);
- Hypergeometrische Verteilung: im Gegensatz zur Binomialverteilung "Ziehen ohne Zurücklegen", dadurch ändern sich die Wahrscheinlichkeiten (z.B. Lotto: eine einmal gezogene Kugel kann nicht noch mal gezogen werden);
- Poissonverteilung: diese wird für seltene Ereignisse mit geringen Wahrscheinlichkeiten (z.B. Autounfälle in einem Ort) verwendet und stellt für diese eine vereinfachende, schnellere Berechnungsform für die auch anwendbare Binomialverteilung dar;
- Geometrische Verteilung: beantwortet die Frage, wie hoch die Wahrscheinlichkeit ist, erst bei der 1., 2., 3. etc. Versuchsdurchführung einen Erfolg zu erzielen.
Stetige Wahrscheinlichkeitsverteilungen
Dazu zählen:
- Normalverteilung: die bedeutendste (stetige) Verteilung, da sie zum einen für viele natürliche Größen (z.B. Körpergröße, Körpergewicht) zutrifft und zum anderen Verteilungen wie die Binomialverteilung u.U. durch die Normalverteilung approximiert werden können;
- t-Verteilung: Alternative zur Normalverteilung, wenn die Varianz bzw. Standardabweichung der Grundgesamtheit nicht bekannt ist;
- Exponentialverteilung: für Lebensdauer- und Wartezeitenprobleme;
- Weibull-Verteilung: für Lebensdauerwahrscheinlichkeiten;
- Stetige Gleichverteilung: für Wartezeitenprobleme.