Extremwerte
Extremwerte Definition
Extremwerte einer Funktion sind Minima (tiefste Punkte, Tiefpunkte) und Maxima (höchste Punkte, Hochpunkte), wobei diese lokal (auf eine bestimmte Stelle bzw. einen bestimmten Bereich bezogen) oder global (auf den gesamten Definitionsbereich der Funktion bezogen) – oder beides gleichzeitig – sein können.
Man kann sich hier ein Gebirge mit mehreren hohen Bergen vorstellen. Man hat den Gipfel des Zweitausender erklommen und damit ein lokales Maximum erreicht. Daneben steht der höchste Berg, ein Dreitausender, dessen Gipfel dann das globale Maximum des Gebirges darstellt.
Lokale Extrema kann man mit folgenden 2 Schritten finden:
- bei lokalen Extrema hat die 1. Ableitung der Funktion den Wert 0; man setzt deshalb die 1. Ableitung der Funktion gleich 0 und erhält damit die Punkte, die lokale Extrema sein können (sog. stationäre Punkte); Warum ist das so? Man stelle sich vor, man zieht mit einem Schlitten einen Schneeberg hoch; solange der Schlitten der Steigung des Berges folgt und schrägt nach oben gerichtet ist, ist die höchste Stelle des Berges nicht erreicht, es geht weiter bergauf. An der höchsten Stelle steht der Schlitten dann waagrecht (die Steigung ist 0) und danach geht es den Berg runter (die Steigung wird negativ). Mathematisch wird die Steigung in einem Punkt durch die 1. Ableitung repräsentiert und wenn man diese gleich Null setzt, hat man eben einen stationären Punkt an der Stelle x erreicht.
- ist dann die 2. Ableitung der Funktion an der Stelle eines stationären Punkts < 0, liegt ein lokales Maximum vor; ist sie größer 0, liegt ein lokales Minimum vor.
Beispiel: Tiefpunkt berechnen
Die Funktion sei f (x) = x2; man könnte z.B. die Funktionswerte für das ganzzahlige Intervall von -2 bis 2, also für die Zahlen -2, -1, 0, 1 und 2 berechnen; die Funktionswerte sind entsprechend 4, 1 0, 1, und 4 und man sieht hier leicht, dass das Minimum bei 0 ist.
Die 1. Ableitung der Funktion ist f '(x) = 2x; diese mit f '(x) = 2x = 0 gleich Null gesetzt ergibt als stationären Punkt nur 0 (2 × 0 = 0). An der Stelle 0 kann also ein lokales Extremum vorliegen.
Die 2. Ableitung der Funktion ist f ''(x) = 2; auch an der Stelle 0 ist sie (wie an allen Stellen) gleich 2: f ''(0) = 2; das ist größer als 0, somit liegt ein lokales Minimum vor. Der Funktionswert an der Stelle ist mit f (0) = 02 hier ebenfalls 0. Das lokale Minimum bzw. der Tiefpunkt liegt also grafisch im Nullpunkt (0, 0) des Koordinatensystems.
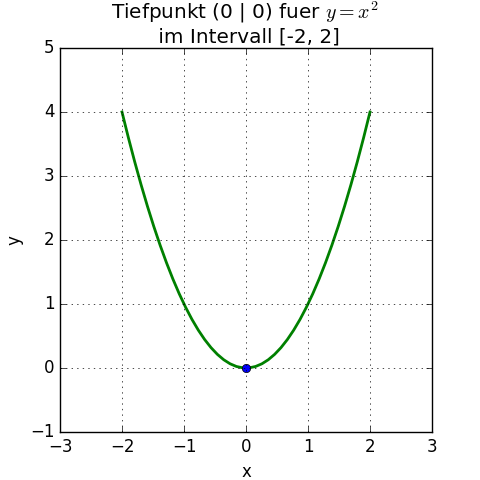
Der Tiefpunkt gilt für f (x) = x2 auch global (durch das Quadrieren sind alle x2-Werte positiv, mit Ausnahme von y = 0 für x = 0 als niedrigstem möglichen Wert).
Beispiel: Hochpunkt berechnen
Die Funktion sei jetzt f (x) = -(x2), wieder ganzzahlig im Intervall von -2 bis 2.
Die 1. Ableitung der Funktion ist f '(x) = -2x; diese mit f '(x) = -2x = 0 gleich Null gesetzt ergibt als stationären Punkt wieder nur 0 (-2 × 0 = 0). An der Stelle 0 kann also ein lokales Extremum vorliegen.
Die 2. Ableitung der Funktion ist f ''(x) = -2; auch an der Stelle 0 ist sie (wie an allen Stellen) gleich -2: f ''(0) = -2; das ist kleiner als 0, somit liegt ein lokales Maximum vor. Der Funktionswert an der Stelle ist mit f (0) = -(02) hier ebenfalls 0. Der Hochpunkt liegt grafisch im Nullpunkt (0, 0) des Koordinatensystems.
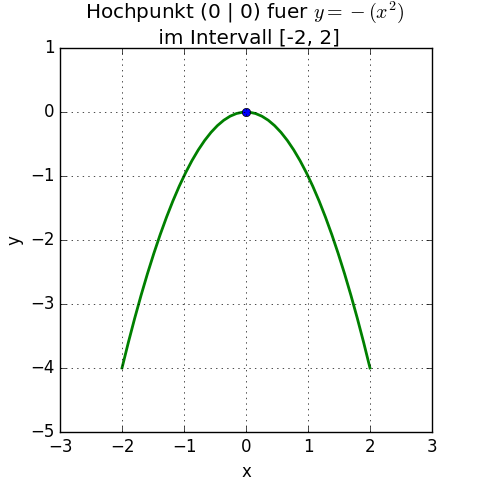
Der Hochpunkt gilt für f (x) = -(x2) auch wieder global (durch das Quadrieren sind alle Funktionswerte positiv, durch das Minus vor dem Term wird das immer ins Negative gekippt, mit Ausnahme von y = 0 für x = 0 als höchstem möglichen Wert).
Alternative Begriffe: Extrema, Extremalstellen, Extrempunkte, Extremstellen.
Keine Extremwerte
Der Versuch, die 1. Ableitung gleich Null zu setzten, ist manchmal erfolglos; dann hat die Funktion keine Extremwerte.
Beispiel: Funktion ohne Extrema
Im Beispiel zur linearen Funktion war die Funktion $f(x) = 2 \cdot x + 20$.
Die 1. Ableitung der Funktion ist f '(x) = 2. D.h., der Funktionswert der Ableitungsfunktion ist immer 2, egal für welches x, also nie 0.
Das bedeutet, die Funktion hat auch kein Maximum oder Minimum. Die lineare Funktion wächst immer weiter, für größere x-Werte werden die y-Werte immer größer. Die lineare Funktion ist sozusagen wie eine Leiter in den Himmel.