Definition
Dreifache Nullstelle bedeutet: Man berechnet Nullstellen einer Funktion und eine Nullstelle kommt dreimal vor.
Alternative Begriffe: 3-fache Nullstelle.
Beispiel
Dreifache Nullstellen erkennt man am besten in der Linearfaktordarstellung bzw. Produktform einer Funktion.
Die Funktion $(x - 1)^3$ kann man auch so mit Linearfaktoren schreiben:
$(x - 1) \cdot (x - 1) \cdot (x - 1)$
Sie hat eine dreifache Nullstelle bei x = 1. Diese setzt den ersten Term (x - 1) gleich 0, den zweiten Term (x - 1) und den dritten Term (x - 1) ebenfalls.
Hat eine Funktion eine dreifache Nullstelle, überquert ihr Funktionsgraph die waagrechte x-Achse (das tut der Funktionsgraph allerdings auch bei einer einfachen Nullstelle).
Bedeutung
Sehen wir uns die obige Funktion als Graph an und erkennen daran Eigenschaften und Folgen einer dreifachen Nullstelle:
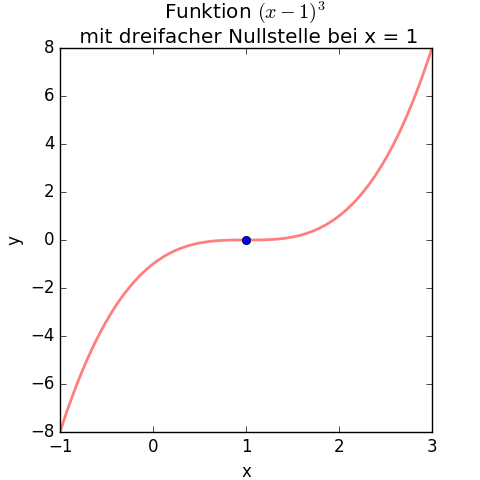
Sattel- bzw. Terrassenpunkt
Hat eine Funktion eine dreifache Nullstelle, hat sie dort einen Sattel- bzw. Terrassenpunkt.
Das ist ein Wendepunkt (ein Punkt, in dem sich das Krümmungsverhalten ändert) mit der zusätzlichen Bedingung, dass die Steigung der Funktion (und somit die 1. Ableitung) an dem Wendepunkt 0 ist.
Vorzeichenwechsel
Der Graph wechselt hier an der (dreifachen) Nullstelle von negativen Funktionswerten zu positiven Funktionswerten (oder umgekehrt bei anderen Funktionen: von positiven Funktionswerten zu negativen Funktionswerten).
Ableitungen
Wenn ein x (hier: x = 1) eine dreifache Nullstelle von f(x) ist, ist sie auch Nullstelle der 1. Ableitung f'(x) und der 2. Ableitung f''(x):
Die 1. Ableitung von $f(x) = (x - 1)^3$ ist:
$f'(x) = 3 \cdot (x - 1)^2$
An der Stelle x = 1 (dreifache Nullstelle):
$f'(1) = 3 \cdot (1 - 1)^2 = 0$
Die 2. Ableitung ist:
$f''(x) = 6 \cdot (x - 1)$
An der Stelle x = 1 (dreifache Nullstelle):
$f''(1) = 6 \cdot (1 - 1)^2 = 0$
Die 3. Ableitung ist:
$f'''(x) = 6$
An der Stelle x = 1 (dreifache Nullstelle):
$f'''(1) = 6$
Die 3. Ableitung ist bei dreifachen Nullstellen immer ungleich 0.
Fazit
- Dreifache Nullstelle: Faktor (x − a)3 in der Linearfaktordarstellung → Nullstelle x = a mit Vielfachheit 3.
- Im Graphen: Kurve überquert die x-Achse (Vorzeichenwechsel) – wie bei einer einfachen Nullstelle.
- An einer dreifachen Nullstelle liegt ein Sattelpunkt (Terrassenpunkt) vor: f′(a) = 0, f′′(a) = 0, f′′′(a) ≠ 0.
- Abgrenzung: Doppelte Nullstelle = kein Vorzeichenwechsel; dreifache = Vorzeichenwechsel mit horizontaler Tangente.
Selbsttest: Dreifache Nullstelle
Aufgabe: Dreifache Nullstelle
Gegeben: f(x) = (x − 2)3. Bestimmen Sie die dreifache Nullstelle und zeigen Sie, dass dort ein Sattelpunkt vorliegt.
Dreifache Nullstelle: (x − 2)3 = 0 → x = 2
1. Ableitung: f′(x) = 3(x − 2)2; f′(2) = 0 ✓
2. Ableitung: f′′(x) = 6(x − 2); f′′(2) = 0 ✓
3. Ableitung: f′′′(x) = 6; f′′′(2) = 6 ≠ 0 ✓
Ergebnis: Sattelpunkt bei (2|0). Vorzeichenwechsel: f(x) < 0 für x < 2; f(x) > 0 für x > 2.