Cobb-Douglas-Produktionsfunktion
Definition
Die Cobb-Douglas-Produktionsfunktion ist eine substitutionale Produktionsfunktion, das heißt, die Einsatzfaktoren (in der Regel Arbeit und Kapital) können gegeneinander ausgetauscht werden.
Formel
Ihre allgemeine Form lautet:
y (K, L)= a × Kα × Lβ.
mit
- y als Produktionsmenge bzw. Output
- K als Einsatzfaktor Kapital
- L als Einsatzfaktor Arbeit (labour)
- a als Konstante
- α als Produktionselastizität des Outputs in Bezug auf K
- β als Produktionselastizität des Outputs in Bezug auf L
Zur Erinnerung: Die (partielle) Produktionselastizität gibt an, wie sich der Output im Verhältnis ändert, wenn sich ein Einsatzfaktor ändert und der andere Einsatzfaktor gleich bleibt.
Beispiel: die Menge des Einsatzfaktors 1 Kapital wird um 1 % erhöht und die Menge des Einsatzfaktors 2 Arbeit bleibt konstant – Um wieviele Prozent erhöht sich der Output?)
Beispiel
y (K, L) = 1 × K0,4 × L0,6.
Testen wir die Funktion mit ein paar Werten:
y (100, 100) = 1 × 1000,4 × 1000,6 = 100
Bei 100 Einheiten Kapital (zum Beispiel Maschinen) und 100 Einheiten Arbeit (zum Beispiel Arbeitsstunden) ist der Output 100 Einheiten.
Erhöhen wir Kapital marginal um eine Einheit und halten Arbeit konstant bei 100:
y (101, 100) = 1 × 1010,4 × 1000,6 = 100,40 (gerundet).
Bei 101 Einheiten Kapital und 100 Einheiten Arbeit ist der Output um 0,4 gegenüber dem Ausgangsniveau gestiegen.
Und ebenso bei weiteren Erhöhungen: eine Einheit mehr Kapital (jetzt von 101 auf 102) bringt 0,4 Einheiten mehr Output:
y (102, 100) = 1 × 1020,4 × 1000,6 = 100,80 (gerundet).
Erhöhen wir nun Arbeit marginal um eine Einheit und halten Kapital konstant bei 100:
y (100, 101) = 1 × 1000,4 × 1010,6 = 100,60 (gerundet).
Bei 100 Einheiten Kapital und 101 Einheiten Arbeit ist der Output um 0,6 gegenüber dem Ausgangsniveau gestiegen.
Isoquanten der Cobb-Douglas-Produktionsfunktion
Die Isoquanten, die alle Kombinationen von Produktionsfaktoren darstellen, die ein und dieselbe Ausbringungsmenge erzeugen, sind Kurven (während sie bei der linearen Produktionsfunktion Geraden und bei der Leontief-Produktionsfunktion L-förmig sind).
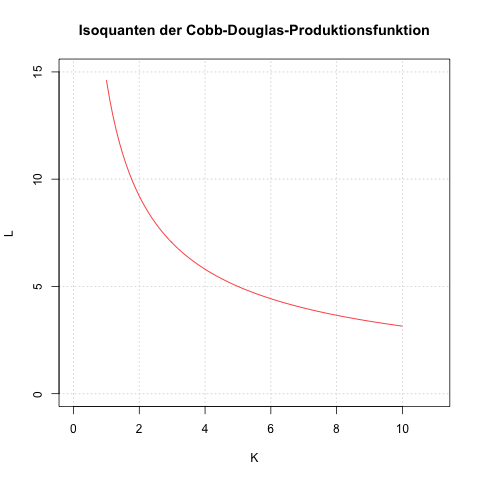
Die Grafik zeigt die Isoquante für das Outputniveau 5. So ist zum Beispiel
- y (K, L) = y (1, 14,62) = 10,4 × 14,620,6 = 1 × 5,00 = 5,00 (gerundet).
- y (K, L) = y (10, 3,15) = 100,4 × 3,150,6 = 2,51 × 1,99 = 5,00 (gerundet).
Diese Punkte liegen auf der Isoquante. Arbeit und Kapital können also in unterschiedlichen Kombinationen zu einem Output von 5 führen, sie können gegeneinander ausgetauscht werden: mehr Kapital, weniger Arbeit oder mehr Arbeit, weniger Kapital. Diese vielen möglichen Kombinationen zeigt die Isoquante an.
Skalenerträge der Cobb-Douglas-Produktionsfunktion
Ist (α + β) > 1, liegen steigende Skalenerträge vor.
Ist (α + β) = 1, konstante Skalenerträge.
Ist (α + β) < 1, sinkende Skalenerträge.
Konstante Skalenerträge wie im Beispiel bedeuten: verdopple ich beide Produktionsfaktoren, verdoppelt sich der Output, zum Beispiel:
y (K, L) = y (20, 6,30) = 200,4 × 6,300,6 = 3,31 × 3,02 = 10,00 (gerundet).
Cobb-Douglas-Produktionsfunktionen erkennen
Das "Hochstellen" der Produktionskoeffizienten α und β und damit das Vorliegen einer Cobb-Douglas-Produktionsfunktion sind nicht immer so eindeutig zu sehen. So kann zum Beispiel $\sqrt{K \cdot L}$ auch als $K^{0,5} \cdot L^{0,5}$ geschrieben werden.