Indifferenzkurve
Definition
Eine Indifferenzkurve in der Mikroökonomie stellt grafisch alle Güterbündel (modellhaft bestehend aus 2 Gütern) dar, die vom Haushalt / Konsumenten gleichgewertet werden bzw. ihm den gleichen Nutzen bringen.
Der Konsument ist indifferent bezüglich der auf der Indifferenzkurve dargestellten Güterbündel (das eine ist ihm gleich lieb wie das andere; es ist ihm egal, welches der Güterbündel er hat).
Indifferenzkurven sind für jeden Haushalt / Konsumenten, je nach Präferenzen, individuell.
Alternative Begriffe: Nutzenindifferenzkurve.
Beispiel
Aufbauend auf dem Beispiel zur Nutzenfunktion:
Diese war U (x, y) = x + 3 × y mit x für die konsumierte Menge von Gut 1 (zum Beispiel Liter Milch) und y für die konsumierte Menge von Gut 2 (zum Beispiel kg Brot).
So haben beispielsweise folgende Güterbündel dasselbe Nutzenniveau von 9:
- 9 Liter Milch, kein Brot: U (9, 0) = 9 + 3 × 0 = 9 + 0 = 9
- 6 Liter Milch, 1 kg Brot: U (6, 1) = 6 + 3 × 1 = 6 + 3 = 9
- 3 Liter Milch, 2 kg Brot: U (3, 2) = 3 + 3 × 2 = 3 + 6 = 9
Verbindet man alle Punkte, die dasselbe Nutzenniveau bieten, erhält man eine Indifferenzkurve.
Für andere Nutzenniveaus (zum Beispiel 10, 11 und 12) können weitere Indifferenzkurven dargestellt werden.
Indifferenzkurve zeichnen
Die Indifferenzkurve für die obige Nutzenfunktion und das Nutzenniveau in Höhe von 9 ist eine Indifferenzgerade (da die Nutzenfunktion im Beispiel eine lineare Funktion ist):
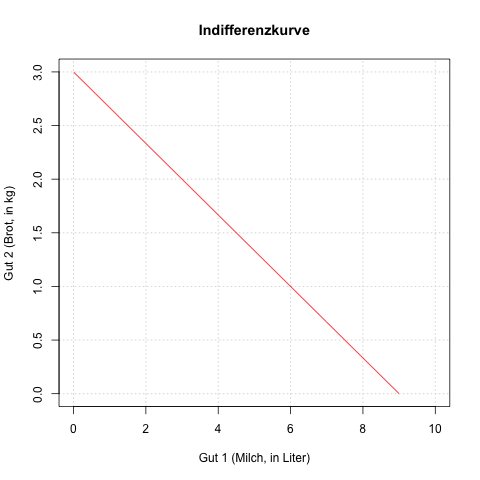
Beispiel: bei einem Wert auf der x-Achse von 6 (Liter Milch) ist der Wert auf der y-Achse 1.0 (kg Brot).
Gleichung der Indifferenzkurve
Die Gleichung der Indifferenzkurve für das Nutzenniveau 9 lässt sich durch ein paar Umformungen bestimmen:
x + 3 × y = 9
3 × y = 9 - x
y (x) = 3 - 1/3 × x
Die Gleichung zeigt den Konsum von y (Brot) in Abhängigkeit vom Konsum von x (Milch) auf einem vorgegebenen Nutzenniveau, zum Beispiel: y (3) = 3 - 1/3 × 3 = 3 - 1 = 2 (bei 3 Liter Milch werden also 2 kg Brot konsumiert, mit einem Nutzenniveau von 9).
Perfekte Substitute
Der Konsument ist bereit, sogenannte perfekte Substitute in einem konstanten Verhältnis zu tauschen, zum Beispiel 1 zu 1.
Beispiel
Eine dazugehörige Nutzenfunktion wäre U (x1, x2) = x1 + x2.
2 Liter Milch und 2 kg Brot würden einen Nutzen von 2 + 2 = 4 stiften.
Tauscht man eins zu eins einen Liter Milch weniger gegen ein kg Brot mehr, ist der Nutzen konstant 1 + 3 = 4.
Perfekte Komplemente
Der Konsument möchte sogenannte perfekte Komplemente in einem konstanten Verhältnis konsumieren.
Beispiel
Jemand trinkt gerne Radler, Bier oder Limo pur mag er nicht; er konsumiert (und mischt) Bier und Limo in einem konstanten Verhältnis (das ergibt eine L-förmige Indifferenzkurve).
Eine dazugehörige Nutzenfunktion wäre U (x1, x2) = min {x1, x2}.
Das heißt, ein Bier und eine Limo sind ihm genauso lieb – haben mit U (1, 1) = min {1, 1} = 1 denselben Nutzen – wie zwei Bier und eine Limo mit U (2, 1) = min {2, 1} = 1.